

- #ARITHMETIC AND GEOMETRIC SEQUENCES CALCULATOR SERIAL NUMBER#
- #ARITHMETIC AND GEOMETRIC SEQUENCES CALCULATOR SERIES#
This formula is used to find the sum of an arithmetic series up to n terms. This formula is used to determine the nth term of an arithmetic series. Here are some formulae that are crucial in order to solve arithmetic progression related problems. But the notations mentioned here are generally widely used. Several sources use different notations for the same terms. The value of n is variable. This notation is not universal. Sn is used to denote the sum of an arithmetic progression from the starting term to the nth term.
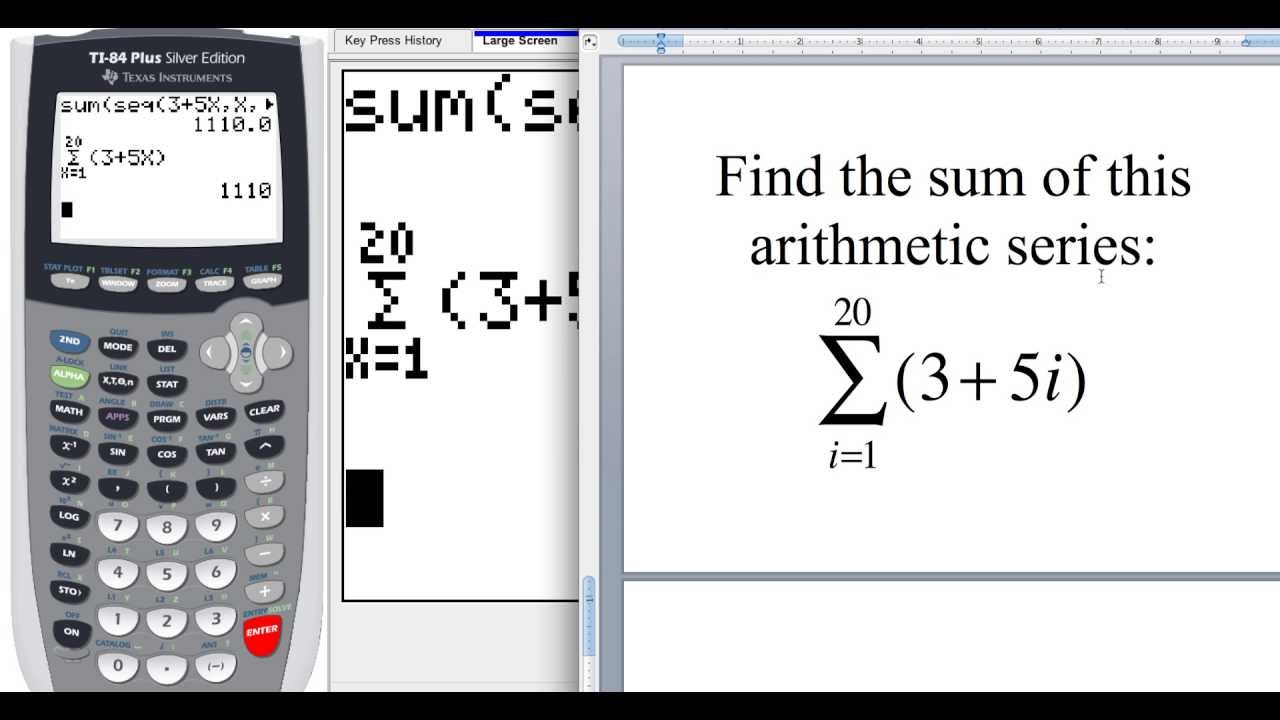
Thus consecutive terms can be represented as a 2 = a 1 + d and so on. The letter ‘d’ denotes the common difference of an arithmetic progression. For example, a 10, denotes the 10 th term in the arithmetic sequence, and a 1 denotes the first term of the sequence.
#ARITHMETIC AND GEOMETRIC SEQUENCES CALCULATOR SERIAL NUMBER#
The subscript of the letter denotes the serial number of the term. The letter ‘a’ denotes a distinct arithmetic sequence. Notation Arithmetic SequenceĪ general arithmetic progression sequence is denoted by a 1, a 2, a 3, ……………., a n, where a 2 – a 1. The series extends from negative infinity to positive infinity. Infinite arithmetic series is an arithmetic progression where the first and last terms are not defined. It is not necessary for an arithmetic progression to have a last term. The last term of an arithmetic progression can be defined when the progression is being defined. The general form of an arithmetic progression is a 1, a 2, a 3, ……………., a n, where a 2 – a 1 is a common difference. It is not necessary that an arithmetic progression has the first term. The first term is usually defined while defining the series. The common difference is defined as the fixed number that has to be added to any term in an arithmetic progression in order to obtain the immediately next number in the sequence.įirst term of an arithmetic progression is the number with which the series starts. Definitions Arithmetic SequenceĪrithmetic progression or Arithmetic Sequence can be officially defined as an arithmetic sequence or progression is defined as a sequence of numbers in which for every pair of consecutive terms, the second number is obtained by adding a fixed number to the first one. Mathematicians such as Paul Turán, Erdős, Endre Szemerédi made further contributions by hypothesizing and proving several theorems related to arithmetic progressions/Sequence. Although there is no evidence of this story, Gauss did make large use of arithmetic progression sequences in his study of discrete mathematics. Gauss is said to have calculated the sum of the first 100 integers when he was 9 without any pen or paper. The first formal study of these sequences was said to be carried out by Carl Gauss, although his first contributions remain largely anecdotal. Arithmetic Sequence is any sequence of numbers in which consecutive numbers vary by a fixed difference.


 0 kommentar(er)
0 kommentar(er)
